AoC Day 23: LAN Party

Graph theory! Cool! In today’s Advent of Code problem, “LAN Party”, we get to identify cliques. This is literate Haskell, imports in the beginning..

import Control.Arrow ((***),(&&&))
import Control.Monad (guard)
import Data.List (intercalate)
import Data.Set (Set)
import qualified Data.Set as Set

Let’s keep things simple and keep identifying the computers as strings. We’ll represent the connection graph with an edge list and an adjacency set.

type Computer = String
data Graph = Graph
  { computers :: ![Computer]
  , connections :: !(Set (Computer,Computer))
  }

Parsing is nothing fancy. I just made the choice to include both edge directions in the set, to simplify lookup.¹

parse :: String -> Graph
parse = uncurry Graph . (Set.elems . Set.unions *** Set.unions) .
        unzip . map parseEdge . lines
  where parseEdge [a1,b1,'-',a2,b2] =
          let c1 = [a1,b1]
              c2 = [a2,b2]
          in (Set.fromList [c1,c2],Set.fromList [(c1,c2),(c2,c1)])

The input is small enough that we don’t need any of the fancy algorithms, we can just iteratively extend the list of N-cliques to N + 1 by checking for all graph edges whether they happen to be connected to all members of a clique under scrutiny.

type Clique = [Computer]
extend :: Graph -> Clique -> [Clique]
extend g [] = pure <$> computers g
extend g cl@(c:_) = do
  c' <- takeWhile (< c) (computers g)
  guard $ all (\c'' -> (c',c'') `Set.member` connections g) cl
  pure (c':cl)

I enforce unicity by generating them ordered.

We can then list all cliques per size.

cliques :: Graph -> [[Clique]]
cliques g = iterate (concatMap (extend g)) [[]]

As expected, most of the content is in the middle.

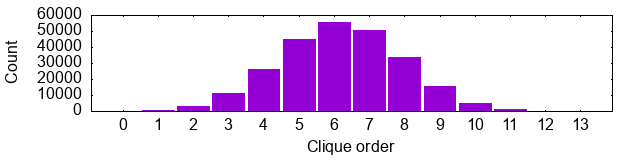
For part 1, we’ll just filter those cliques of order 3 that contain a computer starting in “t”.

part1 :: [[Clique]] -> Int
part1 = length . filter (any ((== 't') . head)) . (!! 3)

For part 2, we’ll just list the last remaining one.

part2 :: [[Clique]] -> String
part2 = intercalate "," . head . last . takeWhile (not . null)

A wrapper and we’re done.

main :: IO ()
main = interact $ show . (part1 &&& part2) . cliques . parse

This concludes today’s solution. See you tomorrow!

It doesn’t simplify the whole: the alternative complexifies lookup by having to either try both directions or enforcing edge ordering, but simplifies parsing.↩︎